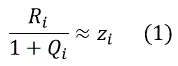
| General information |
| Description |
| Let us have N data points with coordinates xi, yi, zi.The main purpose of this calculation is to obtain a relatively simple formula of data fitting z=f(x,y). We apply the generalized Pade functions for the approximation of data in the following form: |
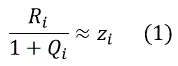
|
|
where R(x, y), Q(x,y) are polynomial functions, Ri and Qi are their values calculated at
i-th point. Pade functions have the following advantages: |
|
|
| You can find an excellent summary of properties of Pade functions here. |
| Methodology |
| The residual sum of squares (RSS) corresponding to (1) is the following |
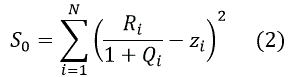
|
| Minimization of S0 leads to a system of nonlinear equations with respect to coefficients of polynomial functions, therefore the equation (1) is presented in the equivalent form |
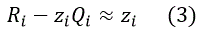
|
| with corresponding RSS |
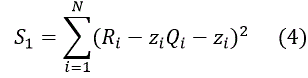
|
|
This new form of RSS yields a system of linear equations.
This idea was efficiently used in paper [2] for 2D data fitting.
For the case of 3D regression analysis we use the following approximation
R(x)=a0+ a1x+ a2y+ a3x2+ a4xy+ a5y2
and Q(x)=b1x+ b2y+ b3x2+ b4xy+ b5y2
if N>11. In this case we have 11 free parameters defined in the calculation by minimization of S1
solving the corresponding linear equations.
In addition we try substitutions X=xqx, Y=yqy, X=exp(ex*x), and Y=exp(ey*y. These four parameters (qx, qy, ex, ey) are calculated by minimizing S0. In all cases we check if the denominator is equal to 0 in the given domain [min{xi}, max{xi}] for variable x and [min{yi}, max{yi}] for y. We discard this solution if it is happened. If N<12 the polynomials are reduced to the form R(x)=a0+ a1x+ a2y and Q(x)=b1x+ b2y |
| Standard deviation SD is calculated |
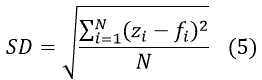
|
| as well as maximum local error |
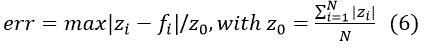
|
|
We suppose that this calculation will be useful for researchers and engineers looking for good approximation of data with simple formula. To check the efficiency of suggested calculation, please see examples. |
| References |
|