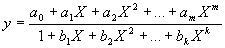
General information
Description
The main purpose of this calculation is obtaining relatively simple formula of data fitting y=f(x). We apply the generalized Pade functions for the approximation of data in the following form:
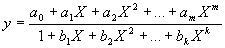
where ai, and bi are coefficients, which should be chosen as the best approximation of given data. We try different values of m and k, and different substitutions X=xq, X=exp(qx) (-1≤ q ≤ 1), and X=log(x) in the program looking for the best approximation.
Pade functions have the following advantages:
  • They have the same or better convergence compared to the power series.
  • They can include functions with singularities, for instance function of the following type:
  • Calculating the Pade function coefficients for given coordinates of points, we have to solve only linear equations.
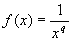
An excellent summary of properties of Pade functions you can find here.
Assumptions
It is assumed that we have enough data for a reasonable approximation. We start to calculate the Pade function coefficients when the number of them is equal to 3, increasing this number until we reach the required accuracy or any other condition of approximation defined by user.
Methodology
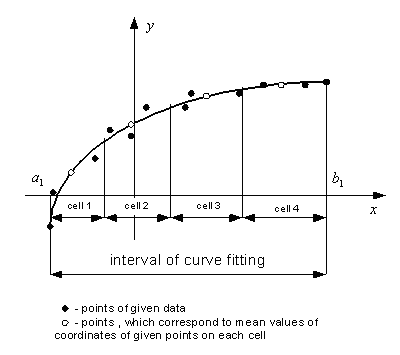
We use two ways of choosing the points, through which the Pade function should pass. In both cases we include two boundary points. Using the first way we also include points, which have coordinates corresponding to the mean values of coordinates of given points that belong to each cell (Fig. 1).
Figure 1. Data and fitting curve of the first way of approximation.
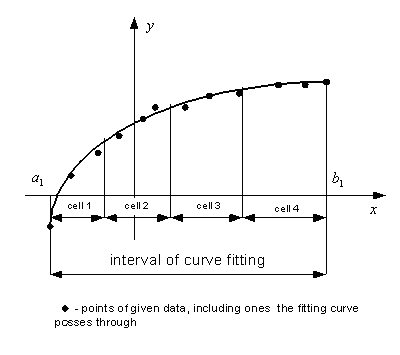
Using the second way, we include one given point from each cell (Fig. 2).
Figure 2. Data and fitting curve of the second way of approximation.
Increasing the number of coefficients of approximation function from 3 until the maximum (or required accuracy) entered by user will be reached and varying the form of approximation function on each step, the program calculates and chooses the best approximation. The criterion is the value of correlation coefficient. The calculation will be completed if one of the following 3 conditions is reached:
  1. When the correlation coefficient is equal to or greater than that entered by user.
  2. When the accuracy of approximation is equal to or less than that entered by user. The accuracy of approximation is calculated as the ratio of the maximum error of approximation to the mean value of absolute values of ordinates of all given points.
  3. When the current amount of coefficients of the approximation function is equal to the maximum entered by user. This condition is important when user prefers to obtain a shorter approximation formula rather than to reach stronger accuracy of approximation.

We suppose that this calculation will be useful for researchers and engineers looking for good approximation of data with simple formula. To check the efficiency of suggested calculation, please see examples.

References
  1. Baker C. , Graves-Morris P., Pade Approximation.