Examples - Trusses

Examples

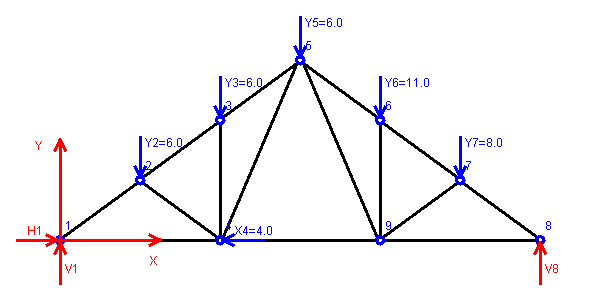
The following example represents truss with 9 joints and 16 members under forces applied to different joints.

Input number of joints:

Number of joints n>2:

Input coordinates of joints:

x₁ :	0	y₁ :	0
x₂ ≥0 :	10	y₂ ≥0 :	7.5
x₃ ≥0 :	20	y₃ ≥0 :	15
x₄ ≥0 :	20	y₄ ≥0 :	0
x₅ ≥0 :	30	y₅ ≥0 :	22.5
x₆ ≥0 :	40	y₆ ≥0 :	15
x₇ ≥0 :	50	y₇ ≥0 :	7.5
x₈ ≥0 :	60	y₈ ≥0 :	0
x₉ ≥0 :	40	y₉ ≥0 :	0

Input truss members:

First end (joint) of member # 1:	1	Second end (joint) of member # 1:	2
First end (joint) of member # 2:	1	Second end (joint) of member # 2:	4
First end (joint) of member # 3:	2	Second end (joint) of member # 3:	3
First end (joint) of member # 4:	2	Second end (joint) of member # 4:	4
First end (joint) of member # 5:	3	Second end (joint) of member # 5:	4
First end (joint) of member # 6:	3	Second end (joint) of member # 6:	5
First end (joint) of member # 7:	4	Second end (joint) of member # 7:	5
First end (joint) of member # 8:	4	Second end (joint) of member # 8:	9
First end (joint) of member # 9:	5	Second end (joint) of member # 9:	6
First end (joint) of member # 10:	5	Second end (joint) of member # 10:	9
First end (joint) of member # 11:	6	Second end (joint) of member # 11:	7
First end (joint) of member # 12:	6	Second end (joint) of member # 12:	9
First end (joint) of member # 13:	7	Second end (joint) of member # 13:	8
First end (joint) of member # 14:	7	Second end (joint) of member # 14:	9
First end (joint) of member # 15:	8	Second end (joint) of member # 15:	9

Input constraints:

Number of joint of horizontal constraint # 1:	1	Number of joint of vertical constraint # 1:	1
Number of joint of horizontal constraint # 2:		Number of joint of vertical constraint # 2:	8

Input vertical and horizontal components of external forces applied to joints:

X₁ :	Reaction	Y₁ :	Reaction
X₂ :		Y₂ :	-6
X₃ :		Y₃ :	-6
X₄ :	-4	Y₄ :
X₅ :		Y₅ :	-6
X₆ :		Y₆ :	-11
X₇ :		Y₇ :	-8
X₈ :		Y₈ :	Reaction
X₉ :		Y₉ :

Output:

The horizontal reaction is: H1=4 . The vertical reactions are: V1=17, V8=20 .

The computed internal forces are: N₁₂=-28.333; N₁₄=18.667; N₂₃=-23.333; N₂₄=-5; N₃₄=-6; N₃₅=-23.333; N₄₅=9.849; N₄₉=14.667; N₅₆=-26.667; N₅₉=16.415; N₆₇=-26.667; N₆₉=-11; N₇₈=-33.333; N₇₉=-6.667; N₈₉=26.667;

Solution
Reactions:
Equilibrium equation of truss with respect to x-axis:
H1=-X₄=+4=4;

Equilibrium equation of truss (the sum of moments about joint with number 8):
V1=(+Y₂(x₂-x₈)+Y₃(x₃-x₈)+Y₅(x₅-x₈)+Y₆(x₆-x₈)+Y₇(x₇-x₈)-X₄(y₄-y₈)-H1(y₁-y₈))/(x₈-x₁)=(-6(10-60)-6(20-60)-6(30-60)-11(40-60)-8(50-60)+4(0-0)-4(0-0))/(60-0)=17;

Equilibrium equation of truss with respect to y-axis:
V8=-Y₂-Y₃-Y₅-Y₆-Y₇-V1=+6+6+6+11+8-17=20;

Internal forces of the truss:
Equilibrium equations of joint with number 1 with respect to y and x axes:
N₁₂v₁₂+N₁₄v₁₄+V1=0;
N₁₂h₁₂+N₁₄h₁₄+H1=0;
After substitution of known values we have the system of linear equations
0.6N₁₂+-0N₁₄+17=0;
0.8N₁₂+1N₁₄+4=0;
The solution of the system: N₁₂=-28.333; N₁₄=18.667
Equilibrium equations of joint with number 2 with respect to y and x axes:
N₂₃v₂₃+N₂₄v₂₄+N₂₁v₂₁+Y₂=0;
N₂₃h₂₃+N₂₄h₂₄+N₂₁h₂₁=0;
After substitution of known values we have the system of linear equations
0.6N₂₃-0.6N₂₄+11=0;
0.8N₂₃+0.8N₂₄+22.667=0;
The solution of the system: N₂₃=-23.333; N₂₄=-5
Equilibrium equations of joint with number 3 with respect to y and x axes:
N₃₄v₃₄+N₃₅v₃₅+N₃₂v₃₂+Y₃=0;
N₃₄h₃₄+N₃₅h₃₅+N₃₂h₃₂=0;
After substitution of known values we have the system of linear equations
-1N₃₄+0.6N₃₅+8=0;
-0N₃₄+0.8N₃₅+18.667=0;
The solution of the system: N₃₄=-6; N₃₅=-23.333
Equilibrium equations of joint with number 4 with respect to y and x axes:
N₄₅v₄₅+N₄₉v₄₉+N₄₁v₄₁+N₄₂v₄₂+N₄₃v₄₃=0;
N₄₅h₄₅+N₄₉h₄₉+N₄₁h₄₁+N₄₂h₄₂+N₄₃h₄₃+X₄=0;
After substitution of known values we have the system of linear equations
0.914N₄₅+-0N₄₉-9=0;
0.406N₄₅+1N₄₉-18.667=0;
The solution of the system: N₄₅=9.849; N₄₉=14.667
Equilibrium equations of joint with number 5 with respect to y and x axes:
N₅₆v₅₆+N₅₉v₅₉+N₅₃v₅₃+N₅₄v₅₄+Y₅=0;
N₅₆h₅₆+N₅₉h₅₉+N₅₃h₅₃+N₅₄h₅₄=0;
After substitution of known values we have the system of linear equations
-0.6N₅₆-0.914N₅₉-1=0;
0.8N₅₆+0.406N₅₉+14.667=0;
The solution of the system: N₅₆=-26.667; N₅₉=16.415
Equilibrium equations of joint with number 6 with respect to y and x axes:
N₆₇v₆₇+N₆₉v₆₉+N₆₅v₆₅+Y₆=0;
N₆₇h₆₇+N₆₉h₆₉+N₆₅h₆₅=0;
After substitution of known values we have the system of linear equations
-0.6N₆₇-1N₆₉-27=0;
0.8N₆₇+-0N₆₉+21.333=0;
The solution of the system: N₆₇=-26.667; N₆₉=-11
Equilibrium equations of joint with number 7 with respect to y and x axes:
N₇₈v₇₈+N₇₉v₇₉+N₇₆v₇₆+Y₇=0;
N₇₈h₇₈+N₇₉h₇₉+N₇₆h₇₆=0;
After substitution of known values we have the system of linear equations
-0.6N₇₈-0.6N₇₉-24=0;
0.8N₇₈-0.8N₇₉+21.333=0;
The solution of the system: N₇₈=-33.333; N₇₉=-6.667
Equilibrium state of joint with number 8:
N₈₉h₈₉+N₈₇h₈₇=0;
After substitution of known values we have
-1N₈₉+26.667=0;
The solution is N₈₉=26.667;

Here h_ij and v_ij are cosine and sine of the angle between x-axis and truss member connecting joints i and j .
They are calculated using formulas: h_ij=(x_j-x_i)/l_ij; v_ij=(y_j-y_i)/l_ij ,
l_ij is the distance between joints i and j (the length of truss member).
For the considered truss: l₁₂=12.5; l₁₄=20; l₂₃=12.5; l₂₄=12.5; l₃₄=15; l₃₅=12.5; l₄₅=24.622; l₄₉=20; l₅₆=12.5; l₅₉=24.622; l₆₇=12.5; l₆₉=15; l₇₈=12.5; l₇₉=12.5; l₈₉=20;
h₁₂=0.8; h₁₄=1; h₂₃=0.8; h₂₄=0.8; h₃₄=-0; h₃₅=0.8; h₄₅=0.406; h₄₉=1; h₅₆=0.8; h₅₉=0.406; h₆₇=0.8; h₆₉=-0; h₇₈=0.8; h₇₉=-0.8; h₈₉=-1;
v₁₂=0.6; v₁₄=-0; v₂₃=0.6; v₂₄=-0.6; v₃₄=-1; v₃₅=0.6; v₄₅=0.914; v₄₉=-0; v₅₆=-0.6; v₅₉=-0.914; v₆₇=-0.6; v₆₉=-1; v₇₈=-0.6; v₇₉=-0.6; v₈₉=-0;