| General information |
| Description |
| The classical problem of thin shell theory - axially symmetric deformation of the clamped spherical shell under concentrated force F applied at the pole of the sphere - is considered. There is an exact solution of this boundary value problem for the case of isotropic shell and small deflections compared to the shell thickness (linear solution). Here we have expanded this solution for orthotropic shells with large deflections (fully reversed ) using new asymptotic approach. The derived asymptotic formulae are simple and can be used effectively for analysis and optimal design of the structure. The result of calculation is force-displacement diagram and maximum stresses depending on the deflection amplitude w0. |

|
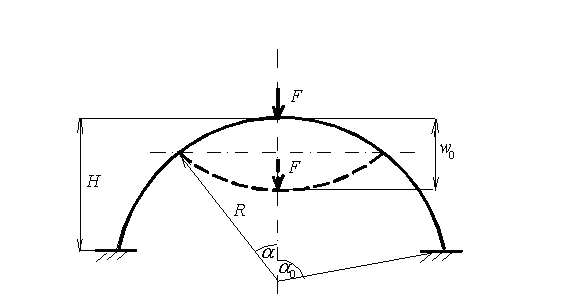
| Figure 1. Clamped orthotropic spherical shell under concentrated force. |
| Assumptions |
|
|
|
| Methodology |
|
The asymptotic formulae derived from the Reissner’s equations are used in the calculation.
The asymptotic analysis is based on the small parameter, which is propotional
to the ratio of the shell thickness to its radius of curvature.
It is important to note that the accuracy of obtained asymptotic results coincides
with the accuracy of the original boundary value problem for a thin shell,
which itself is based on the asymptotic limit of three-dimensional equations
of theory of elasticity with respect to the same small parameter.
Two examples of calculation are shown in the Figure 2 by curves 1 and 2, corresponding to clamped spherical shells with different values of their height H, but the same radius R=0.9. The relevant load-displacement diagram for complete spherical shell is shown by dashed line. |

|
| Figure 2. Force dependance on deflection amplitude of the shell. |
|
The finite element method was used for validation of the asymptotic solution
and calculation. We calculated displacements and stresses for the isotropic structure
with the following properties: radius of the spherical shell R=0.9;
its height H=0.9 and H=0.45; constant thickness h=0.01;
modulus of elasticity E=258000 and Poisson’s ratio of material ν=0.5.
These properties correspond to the cases shown in the Figure 2 by curves 1 and 2.
There is a perfect agreement between asymptotic and numerical solutions on the
whole range of deflection amplitude.
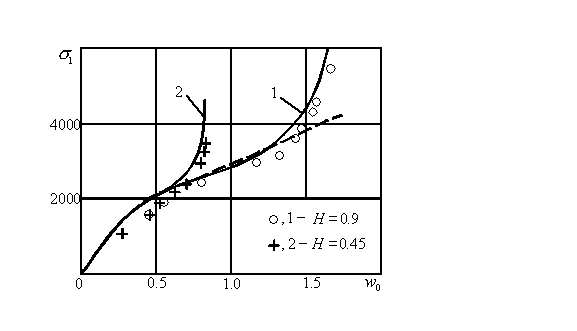
The comparison of maximum bending stresses calculated for the same structures using both numerical and asymptotic methods is shown in the Figure 3. Here also the result of finite element analysis is marked by points. Numerically obtained stresses are slightly smaller than the asymptotic ones. The difference became smaller for larger deflections or thinner shells. |
|
| Figure 3. Bending stresses of spherical shells. |
|
We suppose that this calculation will be valuable for the investigation of the
influence of geometrical and stiffness parameters of the structure on its behavior
and optimal design.
For some comments or more information about calculation of nonlinear behavior of thin shells of different shapes and boundary conditions, geometrical and stiffness properties, and under different types of load please contact the author of the asymptotic method and present calculation Alex Yevkin by email and take a look at his personal web site. |
| References |
|