
| General information |
| Description |
|
It is shown in [1] that in general case parameter estimation of g-renewal process is an ill-posed problem.
It means that the obtained solution cannot be unique and it significantly depends on small changes in the input data.
Previous numerical experiments have shown that the solution sometimes significantly depends on initial parameter values
selected for the iteration methods and the process can converge to different local minimum (maximum) values especially,
if shape parameter of Weibull distribution is close to 1. Therefore the calculation procedure requires a special sophisticated approach.
Typically, additional information is required to resolve the ill-posed problem. It is suggested in [1] to solve the problem in two steps.
At the first step, only underlying life time distribution function parameters are calculated using information
about times of first failure of items. At the next step, only restoration factor q is calculated using all recurrent event times.
Obviously, this approach not only converts ill-posed problem into a regular one, but also is very efficient in terms of computation time,
because estimated parameters are decoupled and at the second step (the most time consuming) only one parameter is calculated.
This approach works well when parameters of underlying probability function are calculated at the first step with good accuracy,
which means that we have information about enough amount of items under observation.
We suggest an improvement of this approach in this online calculation. We developed two methods: least residual sum of squares (RSS) and maximum likelihood estimator (MLE) [2]. The RSS calculation is based on the non-parametric estimate of the cumulative intensity function (CIF). In the MLE method we used raw times between failures as input data. We applied the Newton-Raphson iteration method in case of MLE and the Gauss-Newton algorithm for RSS method. For CIF calculation we applied the advanced Monte Carlo method [3]. Brief description of the advanced Monte Carlo method can be found here. Let us consider the RSS method. To apply it, we have to calculate CIF at each event time using non-parametric estimation. For this purpose we sorted all recurrence and censoring times (ages). If a recurrence age for an item is the same as its suspension age, then the recurrence time goes first. If multiple units have a common recurrence time, then they are shifted slightly, so that at any time only one event occurs. Then we calculated CIF using the following formula |

|
|
where r=ri-1 if ti is recurrence time, r=ri-1-1 if ti is censoring time,
r1=m, which is the total number of items in the test.
Parameter a=1 in all cases except the case when ti corresponds to the very first failure in the test. In this case a=0.5.
This value better fits the obvious condition CIF(t)≈F(t) for small CIF (according to non-parametric estimation
for underlying failure probability function F(t)).
According to [1], we calculated the parameters of underlying lifetime function taking into account only first failures (the standard ranking regression method). The solution delivers minimum value of function S1 corresponding to RSS of Weibull prediction method. At the second step, we are looking for the minimum of function S2 (RSS based on CIF) with respect to restoration factor only. On the other hand, S2 also depends on the lifetime distribution function parameters and CIF is an additional important piece of information which can be used to calculate these parameters more accurately. Therefore we have added another (third) step to the calculation. At this step we are looking for the minimum of function S=S1+S2 depending on restoration factor as well as on lifetime function parameters. We take the solution of the second step as initial values for the final step. The sequence of three steps is a relatively fast converging procedure. We use similar approach for MLE. It is remarkable that the log-likelihood function L of g-renewal process includes the log-likelihood function L1 of Weibull prediction method as a term. Therefore in our procedure we obtain the solution for the maximum of this term at the first step, then for the fixed parameters of the underlying distribution function we find the maximum of L and finally using the obtained solution as the initial one for the next iteration step we calculate all g-renewal parameters corresponding to the maximum of function L. We also studied the influence of Mean Time to Repair (MTTR) on CIF of the g-renewal process. Some brief description of the method can be found here and in [3]. In previous research the authors used the condition that MTTR is much smaller than Mean Time to Failure (MTTF). Approximately, it should be MMTR/MTTF<0.02. Our model allows significantly less strong constraint MTTR/MTTF<0.2. This expansion of the model is especially important for imperfect repair because time to next failure is decreasing with the number of failures and therefore the influence of MTTR is increasing.
Confidence bounds |

|
| where pi g-renewal process parameters: two of them are parameters of the underlying lifetime function and the third parameter is the restoration factor. The corresponding inverse matrix defines the variance-covariance matrix which is used for confidence bounds estimation in our calculations. If bij are elements of this matrix, then the variance of CIF function is calculated as |
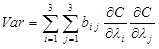
|
| We used the advanced Monte Carlo method for numerical calculation of partial derivatives of CIF with respect to g-renewal process parameters. This calculation requires accurate estimation of CIF and therefore is the most time consuming. The corresponding confidence bounds for CIF are calculated as |

|
|
where α is the desired confidence level.
1.V. Krivtsov and O. Yevkin “Estimation of G-renewal process parameters as an ill-posed inverse problem”,
Reliability Engineering & System Safety, Vol. 115, 2013, pp. 10-18.
|